Last time we derived the following Lagragian
\begin{equation} L = \sum_{i}^{N}\left( \frac 12 m_i \dot x_i^2 - m_i x_i \right) +F x_1 -\sum_{i=2}^{N}\frac{q}{\gamma - 1} \frac{1}{(x_{i+1} - x_i - \ell_{i})^{ \gamma - 1 }} \end{equation}
Where all the the parameters and variables are unitless. Let’s a deeper look at this Lagragian. One thing that stands out is the form of the air compression energy. It only depends on the difference of position variables of the form $x_{i} - x_{i-1}$. Let’s introduce $N-1$ new variables $w_{i} := x_{i} - x_{i-1}$ for $2 \leq x\leq N$ and $w_1 := x_1$. We are left with a new Lagragian
\begin{equation} L = \sum_{i=1}^Nm_i \left( \frac 12 \left( \sum_{j = 1}^{i} \dot w_i \right)^2 - \sum_{j = 1}^{i} w_i \right) +F w_1 -\sum_{i=2}^{N}\frac{q}{\gamma - 1} \frac{1}{(w_i - \ell_{i})^{ \gamma - 1 }} \end{equation}
The first kinetic energy term becomes $\frac12 M_{ij} \dot w_i \dot w_j$ where
\begin{equation} M_{ij} = \sum_{k = \max(i, j)}^N m_k ~. \end{equation}
The gravitational energy can be expressed as $w_i M_i$ where we can write $M_i$ as
\begin{equation} M_i = \sum_{k = i}^{N} m_k \end{equation}
So we have the following Lagrangian
\begin{equation} L = \frac 12 \dot w_i M_{ij} \dot w_j - M_i w_i +F w_1 -\sum_{i=2}^N\frac{q}{\gamma - 1} \frac{1}{(w_i - \ell_{i})^{ \gamma - 1 }} \end{equation}
Translational Symmetry
One symmetry possible stands out here. If we translate in the $w_1$ direction (so $w_1 \to w_1 + a$) our Lagragian changes by this amount.
\begin{equation} \delta L = - M_1 a + F a \end{equation}
We can see this translation is a symmetry if $M_1 = F$. We can see that $M_1$ is just the total mass of all the masses. So we can see if we have the external force balancing out the total weight, we have this symmetry.
Stability
Let’s see if our system has an stable points. Taking the gradient of the potetial energy we get
\begin{equation} \frac{ \partial U }{\partial w_i} = M_i - F \delta_1^i - \frac{q }{(w_i - \ell_{i})^\gamma}(1-\delta_1^i) \end{equation}
To find the critical points we set this gradient to zero. So, we get two sets of equation.
For $\frac{\partial U}{\partial w_1}$,
\begin{equation} M_1 = F \end{equation}
For $\frac{\partial U}{\partial w_i}$ where $i\geq 2$,
\begin{equation} M_i = \frac{q }{(w_i - \ell_{i})^\gamma} \end{equation}
Solving for $w_i$ where $i\geq 2$, we find.
\begin{equation} w_i = \left( \frac{q}{M_i} \right)^{1/\gamma} + \ell_{i} \end{equation}
But we cannot solve for $w_1$, so what should we do? We can see that essntially the independence of $w_1$ in the equation tells that there is no way to find a configuration with certain $w_1$’s. But it does tell us for a certain $F$ we can achieve stability. Such $F$ satifies $F=M_1$. This is the same $F$ to allow use to have symmetry in the $w_1$ direction!
We could also consider “stability” as for only $w_i$ where $i\geq2$. These coordinates are the relative coordinates of our masses. Like some sort of internal coordinates. In that case there would be no need for applying restrictions to $F$.
Now let’s do our due diligence and check if the critical point is a minimum (ie is stable). Staking the second derivative we see we get a diagonal matrix where the off diagonal enerties are zero or positive So in the $w_{i\geq 2}$ direction we have stability. The $w_1$ direction can drift or is not stable.
Perturbations
Let’s look at small oscillations around the equilibrium point. We’ll consider small oscillations as $\varepsilon u_i(t)$ where $\varepsilon \ll 1$. So perturbations would be $w_i = w_{\mathrm{equi}, i} + \varepsilon u_i$. Plugging these $w$’s in to the Lagrangian and expanding to second order, we get.
\begin{equation} L \approx U_{\mathrm{min}} + \frac { \epsilon^2 }2\left( \dot u_i M_{ij} \dot u_j + \sum_{i=2}^N q u_i^2 \gamma \left(\frac{M_i}{q}\right)^{ ( \gamma + 1 )/\gamma } \right) \end{equation}
Finding the characterisic frequencies, it’s interesting to see that the higher frequencies, the lower the and less of the $w$’s you excite. The “higher” you are in the $w$’s the less frequent.
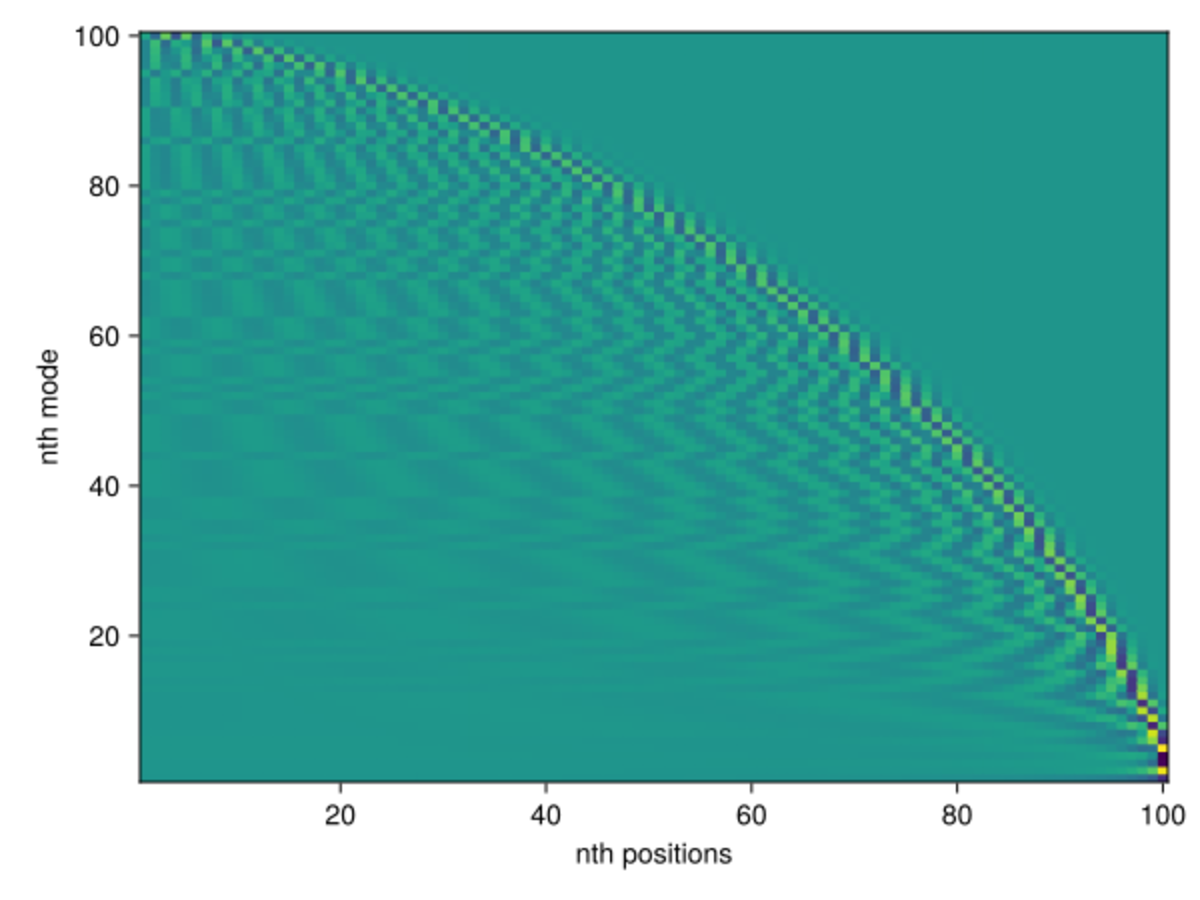
About $M_{ij}$
The mass matrix $M$ has some interesting properties. It’s inverse is simple.
\begin{equation} M_{ij}^{-1} = -\frac{\delta_{i+1, j}}{m_i} - \frac{\delta_{i, j+1}}{m_j} + \delta_{ij} \left(\frac{ 1 }{m_{i}} + \frac{ (1-\delta_{i1}) }{m_{i-1}}\right) \end{equation}
For example for $N=4$ we have
\begin{equation} M^{-1} = \begin{pmatrix} \frac{1}{m_1} & -\frac{1}{m_1} & 0 & 0 \\ -\frac{1}{m_1} & \frac{1}{m_2}+\frac{1}{m_1} & -\frac{1}{m_2} & 0 \\ 0 & -\frac{1}{m_2} & \frac{1}{m_3}+\frac{1}{m_2} & -\frac{1}{m_3} \\ 0 & 0 & -\frac{1}{m_3} & \frac{1}{m_4}+\frac{1}{m_3} \\ \end{pmatrix} \end{equation}
$\mathrm{det}(M) = \prod_i^N m_i$. So interestingly enough there is a family of $M$ matricies with $\mathrm{det} = 1$.