I was watching a YouTube video ¹. The video was about the speed of light in a medium, and I thought it would be interesting to do some relaxing programming with Julia. Specifically, I would like to simulate some light propagating through media with varying dielectric properties. This post will follow these steps:

1. Derive the equations from Maxwell’s equations in a dielectric.
2. Simulate the wave equations.
3. Explore!

From Maxwell’s Equations

Here are Maxwell’s equations as known in a dielectric in general³.

\begin{equation} \nabla \cdot (\varepsilon_0 \mathbf{E} + \mathbf{P}) = \rho_{\text{free}} \end{equation}

\begin{equation} \nabla \cdot \mathbf{B} = 0 \end{equation}

\begin{equation} \nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t} \tag{Faraday} \end{equation}

\begin{equation} \nabla \times \mathbf{B} = \mu_0 \mathbf{J}_{\text{free}} + \mu_0 \frac{\partial}{\partial t}(\varepsilon_0 \mathbf{E} + \mathbf{P}) \end{equation}

We are just concerned with free traveling waves, so the free current and charge densities can be set to vanish.

\begin{equation} \nabla \cdot (\varepsilon_0 \mathbf{E} + \mathbf{P}) = 0 \end{equation}

\begin{equation} \nabla \times \mathbf{B} = \mu_0 \frac{\partial}{\partial t}(\varepsilon_0 \mathbf{E} + \mathbf{P}) \end{equation}

Furthermore, let’s consider a linear dielectric. The polarization is given by $\mathbf{P} = - \varepsilon_0 \chi (x) \mathbf{E}$, and the equations transform to the following.

\begin{equation} \nabla \cdot \varepsilon_0 (\mathbf{E} - \chi (x) \mathbf{E}) = 0 \tag{Gauss 1} \end{equation}

\begin{equation} \nabla \times \mathbf{B} = \mu_0 \varepsilon_0 (1 - \chi (x)) \frac{\partial}{\partial t}\mathbf{E} \tag{Ampere} \end{equation}

The keen-eyed might have noticed that $\chi$ is left to be variable along the $x$ direction. This leads to the possibility of (Gauss 1) having a bound charge induced by the variation of $\chi$. To keep our lives easy, we can consider light with polarizations that point orthogonal to $x$, which can be in any direction in the $y-z$ plane. For definiteness, let’s choose polarization in the $y$ direction. This allows for further simplification.

\begin{equation} \nabla \cdot \mathbf{E} = 0 \tag{Gauss 2} \end{equation}

Now we can take the time derivative of (Ampere) and substitute in (Faraday).

\begin{equation} \nabla \times \frac{\partial}{\partial t} \mathbf{B} = \varepsilon_0 \mu_0 (1 - \chi (x)) \frac{\partial^2}{\partial t^2}\mathbf{E} \end{equation}

\begin{equation} - \nabla \times \nabla \times \mathbf{E} = \mu_0 \varepsilon_0 (1 - \chi (x)) \frac{\partial^2}{\partial t^2}\mathbf{E} \end{equation}

The curl of curl can be rewritten, and then we can apply (Gauss 2).

\begin{equation} - \left(\nabla (\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E}\right) = \mu_0 \varepsilon_0 (1 - \chi (x)) \frac{\partial^2}{\partial t^2}\mathbf{E} \end{equation}

\begin{equation} \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 (1 - \chi (x)) \frac{\partial^2}{\partial t^2}\mathbf{E} \end{equation}

Let’s use natural units (i.e., $c=1$), so this equation becomes

\begin{equation} \frac{1}{1 - \chi (x)} \nabla^2 \mathbf{E} = \frac{\partial^2}{\partial t^2} \mathbf{E}. \end{equation}

Effectively, $(1 - \chi (x))$ is the fraction of the speed of light squared in these units. This means if our light propagates with some velocity $v$ in a dielectric, its speed can be expressed as $(v/c)^2 = 1 - \chi \implies v = c \sqrt{1 - \chi}$, where we restrict $v \lt 1$.

\begin{equation} v^2 \nabla^2 \mathbf{E} = \frac{\partial^2 \mathbf{E}}{\partial t^2}. \end{equation}

We are just interested in $\mathbf{E} = \mathbf{E}^y \mathbf{e}_y$ with only $(t, x)$ dependence.

\begin{equation} v^2 \frac{\partial^2 \mathbf{E}^y}{\partial x^2} = \frac{\partial^2 \mathbf{E}^y}{\partial t^2} \end{equation}

With abuse of notation, we can write

\begin{equation} v^2 \frac{\partial^2 E}{\partial x^2} = \frac{\partial^2 E}{\partial t^2}. \end{equation}

In general, solutions to this equation take the form

\begin{equation} E(t,x) = f_r(x-vt) + f_l(x+vt) \tag{Wave} \end{equation}

Boundary Condition

To simulate this in Julia⁴, we have to truncate the domain since computers have yet to have infinite memory. We can simply have outgoing boundary conditions at the left and right spatial domain. Notice in (Wave), there are two functions. With some thought, one can realize that $f_r$ ($f_l$) represents waves that move right (left)⁵. So, we can restrict our wave equation to move left at the left boundary of the spatial domain and right at the right side.

\begin{equation} \begin{aligned} E(t,x_l) &= f_l(x_l + vt) \ E(t,x_r) &= f_r(x_r - vt) \end{aligned} \end{equation}

This implies in terms of derivatives that

\begin{equation} \begin{aligned} E^{(1,0)}(t,x_l) &= v E^{(0,1)}(t,x_l) \ E^{(1,0)}(t,x_r) &= -v E^{(0,1)}(t,x_r) \end{aligned} \end{equation}

Simulate the Wave Equations

We are ready to simulate the wave equation in Julia. Concretely, we need to use the three following equations.

\begin{equation} \begin{aligned} v^2 \frac{\partial^2 E}{\partial x^2} &= \frac{\partial^2 E}{\partial t^2} \ v E^{(0,1)}(t,x_l) &= E^{(1,0)}(t,x_l) \ -v E^{(0,1)}(t,x_r) &= E^{(1,0)}(t,x_r) \end{aligned} \end{equation}

In order to simulate such equations, we need to discretize the spatial variable $x$ and the temporal variable $t$. To make it simple, let’s use an equidistant/equitemporal discretization.

So for (x), we will restrict (x) to (x \in [-1, 1]) where (x) can only take values indexed by (i \in {1, \ldots, N}) and (x_i = 2(i-1)/(N-1) - 1).

In Julia, you can write this with:

function make_grid(n)
    return collect(range(-1, 1, length=n))
end

With this grid, we would like to discretize (\partial^2 E/\partial x^2). One way is with finite differencing, which is the definition of derivatives but without the (\mathrm{lim}). For the second derivative, we use (Approx 2nd 1):

\begin{equation} \tag{Approx 2nd 1} E’’(x) \approx \frac{E(x+h) - 2E(x) + E(x-h)}{h^2} \end{equation}

where (h) is the distance between two grid points. We can also write the second derivative as (Approx 2nd 2):

\begin{equation} \tag{Approx 2nd 2} \begin{aligned} E^{\prime\prime}(x_i) &\approx \frac{E(x_{i+1}) - 2E(x_{i}) + E(x_{i-1})}{h^2} \ &\approx \frac{E_{i+1} - 2E_{i} + E_{i-1}}{h^2} \end{aligned} \end{equation}

For the first derivative for later use:

\begin{equation} \tag{Approx 1st} E^{\prime}(x_i) \approx \frac{E_{i+1} - E_{i}}{h} \end{equation}

where (h = x_{i + 1} - x_i). ⁶

function dd(E, h)
    ddE = similar(E)
    for i in 2:length(E)-1
        E1 = E[i-1]
        E2 = E[i]
        E3 = E[i+1]
        ddE[i] = (E1 - 2 * E2 + E3) / h^2
    end
    return ddE
end

There is a problem, though: we do not have (E_{0}) nor (E_{N+1}), so this finite difference formula cannot find the second derivative for the endpoints.

To solve this, we will replace the wave equation at the (x) bounds with the boundary equations.

struct ElectricField{T}
    pos::T
    vel::T
end

function time_step(e::ElectricField, dt, h, eps = 1)
    # Update position based on velocity and time step.
    newpos = e.pos + dt * e.vel 
    
    # Update velocity based on spatial derivative and eps.
    # The .* operator is used for element-wise multiplication.
    newvel = e.vel + dt * eps .* dd(e.pos, h)
    
    # Boundary condition at start: adjust first velocity based on eps and
    # spatial step size (h), considering first two positions.
    newvel[begin] = sqrt(eps[begin]) * (e.pos[begin+1] - e.pos[begin]) / h 
    
    # Boundary condition at end: adjust last velocity similarly, using
    # positions at the end.
    newvel[end] = -sqrt(eps[end]) * (e.pos[end] - e.pos[end-1]) / h 
    
    # Return updated ElectricField object with new position and velocity.
    return ElectricField(newpos, newvel)
end

Explore Wave Propagation in Different Media

Finally, we can simulate the propagation of (E). There are a few cases I personally would like to look at, but feel free to mess around with the Pluto Notebook.

The animations use two colors to differentiate the conditions:

• Blue represents light traveling in a vacuum.
• Orange (if displayed) represents light as it travels through a medium with a dielectric applied, in which the speed of the light wave is different.

Remember that units are in natural units. The y-axis represents $E$ and the x-axis represents $x$.

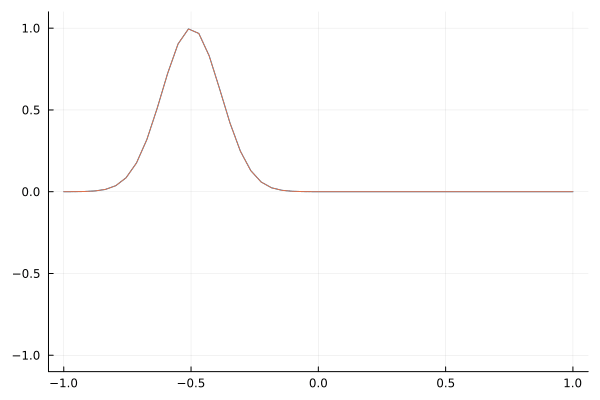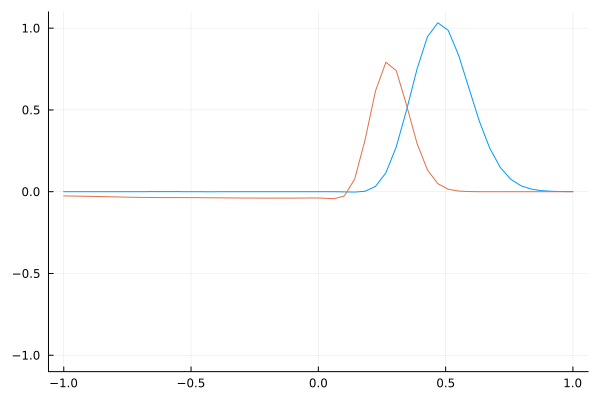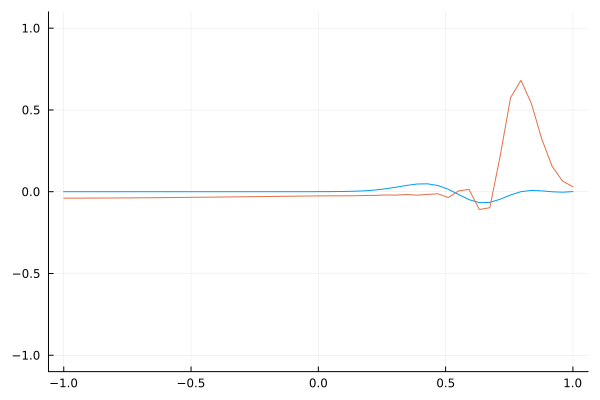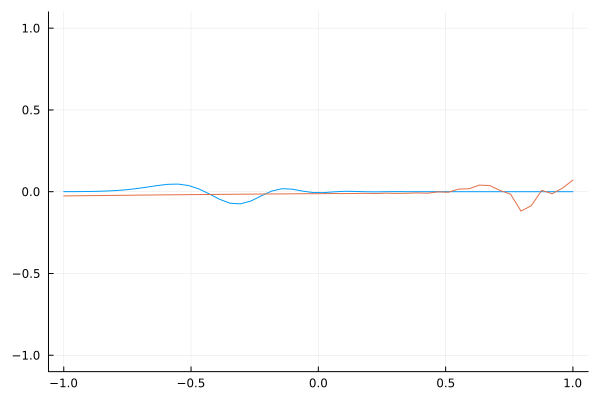
Simple Wave Propagation

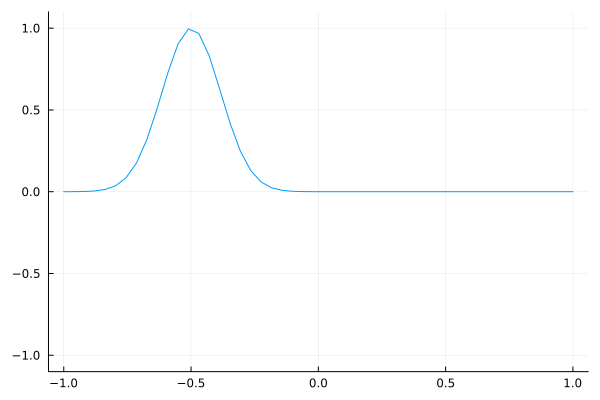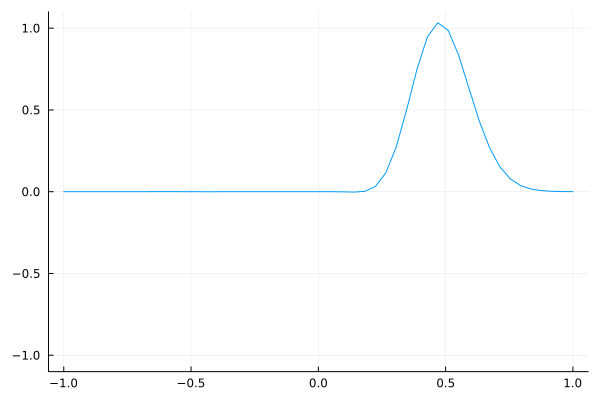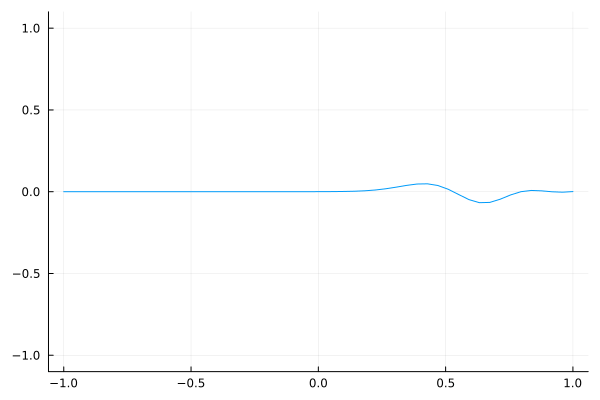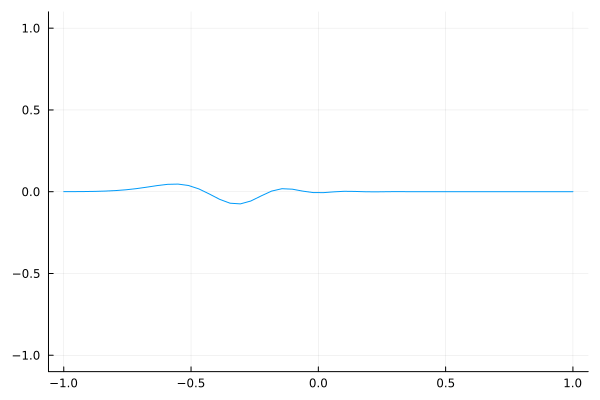
As a sanity check, here is a simple Gaussian wave packet that travels to the right.

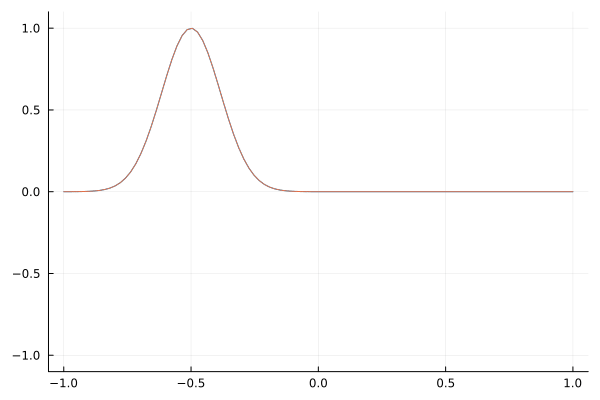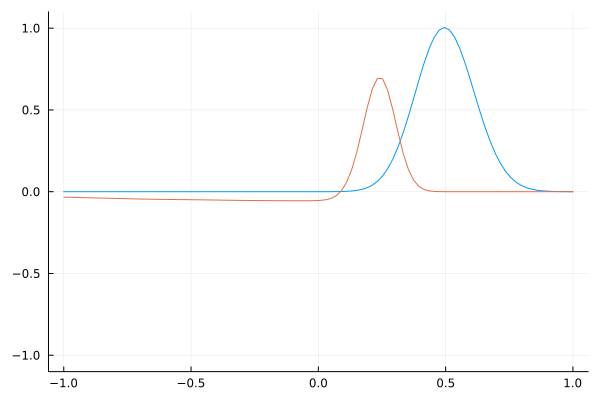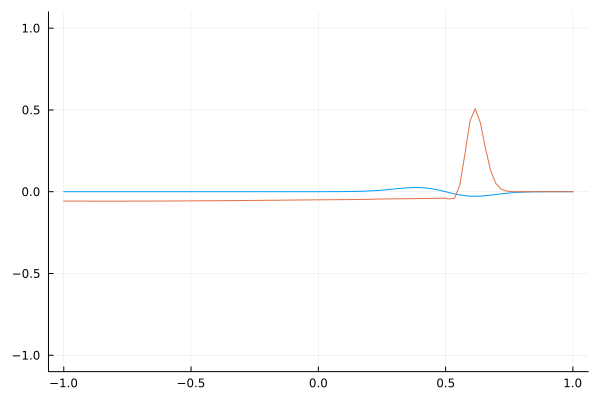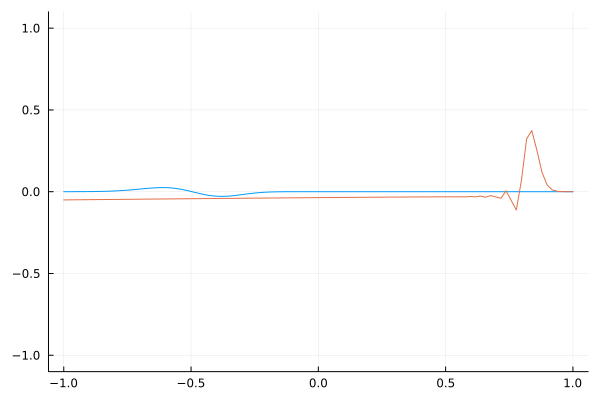
Dielectric Constant Boundary

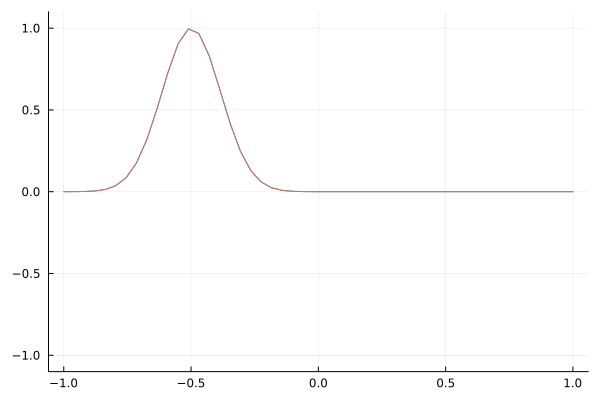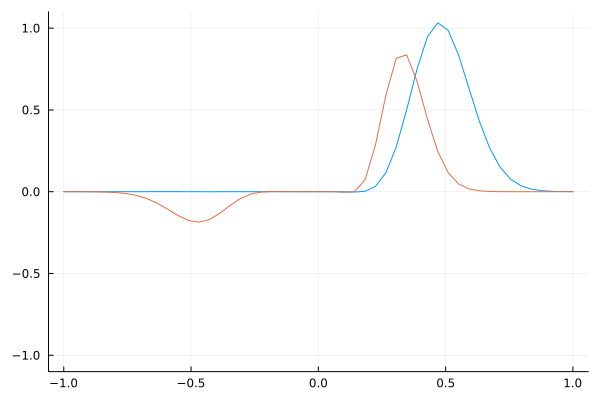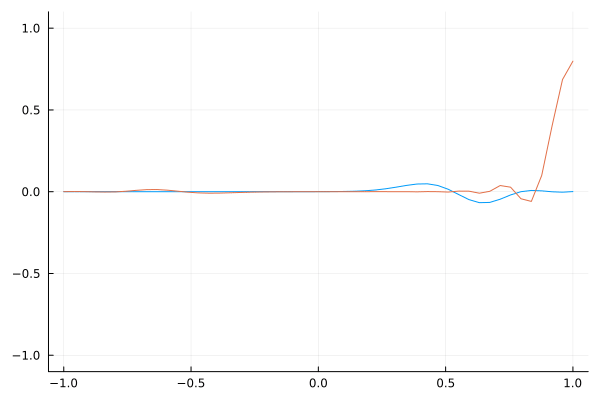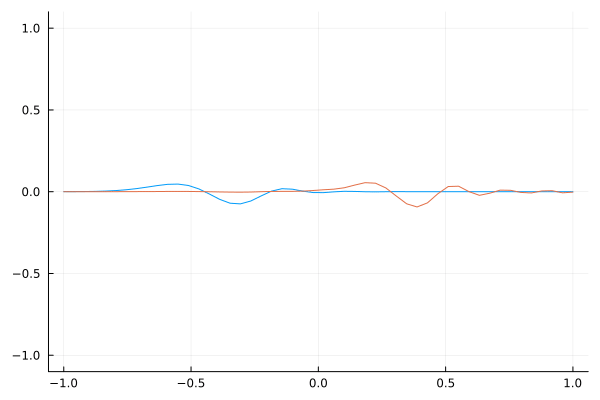
Observe the effect of a sudden change in the dielectric constant at a boundary. It is interesting to see that a simple change in wave speed causes reflection.

“Tanh” $v^2$ Profile

What about a medium that does not abruptly change the wave speed but changes it gradually? We can use

$$v^2(x) = \frac{v^2_f - v^2_i}{2} \tanh(3x) + \frac{v^2_f + v^2_i}{2}~.$$

$v^2$ Profile 1.0 to 0.2

For the first profile, the speed slows down. An interesting observation is that compared to the abrupt change, the reflected wave is more spread out. In other words, the reflected wave seems to have a much longer wavelength.

$v^2$ Profile 1.0 to 0.0

An extreme example is to send the wave speed to zero. One can see that the impinging wave seems to eventually vanish at the left boundary. A more physical mirror could be represented by this since a perfect mirror would not allow light to propagate into it because all of it is reflected. In other words, the light cannot travel into it (speed = 0).

This animation takes the modulation further, transitioning the dielectric properties from 1 to almost 0. It highlights extreme conditions and their dramatic effects on wave propagation.

Tanh $v^2$ Profile From 1 to FTL (Faster Than Light)

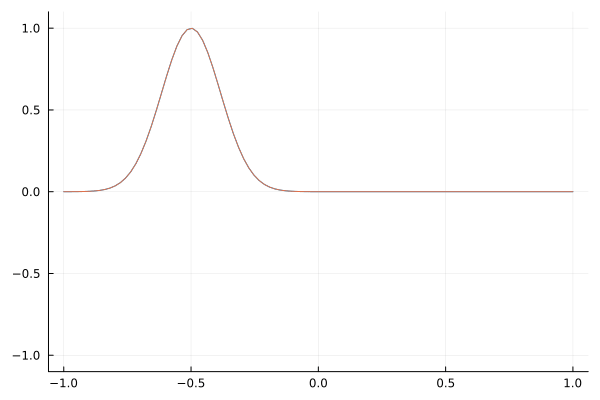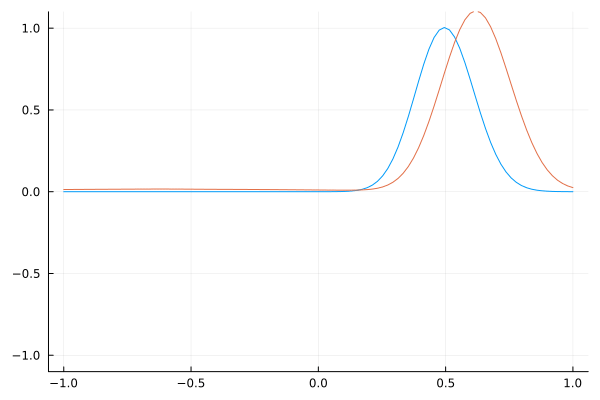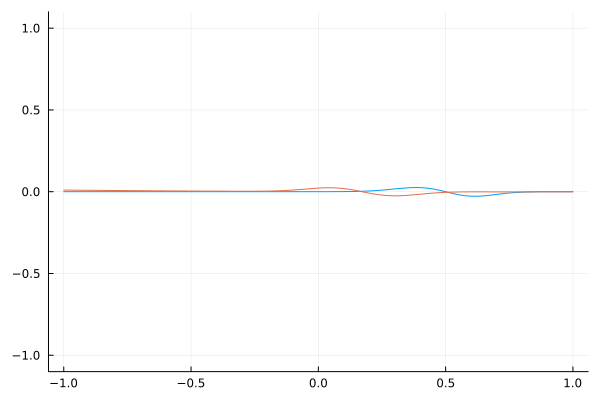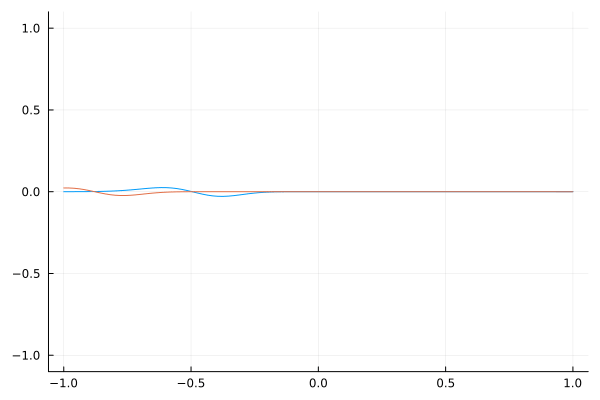
This scenario imagines a transition from normal light speed to conditions supporting faster-than-light (FTL) travel. The obvious speed-up is apparent, but there are two interesting observations: the reflection is minimal, and the magnitude of the $E$ field increases. According to the Poynting vector, this increase in field magnitude corresponds to more energy flux. So, it seems like the medium that light travels through has energy stored in it! For $v^2 \rightarrow \infty$, would the energy flux go to infinity?

I think I could go on for days tinkering with this, but I will let the reader have their fun. Even though this system was simple⁷, I think some interesting results surfaced. Thanks for reading!

Read More

• Videos Code Repo
• Pluto Notebook